Basics of Distributed Systems theory
In this introductory post on distributed systems we'll see some basic concepts such as: local and global states, consistent and inconsistent cuts, vector clocks, Chandy-Lamport's snapshot protocol.
No need for much imagination: we can say that a distributed system is composed of a number of processes that use the same protocol to communicate with each other in order to solve a common problem.
These processes may be on different networks (as in this image) or in the same network. Each process may or may not have different roles; this depends on the protocol.
In a distributed system we don’t have a central point of failure, sure, but it opens the door to a whole other set of complicated issues that need to be handled, for example:
- We might lose messages.
- The network might be slow.
- Some nodes might die.
- Some nodes might behave strangely.
This brings us to a very simple classification of processes and systems.
Taxonomy systems and processes
A system can be:
- Synchronous: processes have a global, reliable “clock”; there is a time bound on message times.
- Asynchronous: we don’t have a divine global clock; we don’t know how long messages take to arrive.
As for processes, we can classify them by the ways they can fail:
- Crash-faulty: they can crash.
- Bizantine: buggy or malicious; unreliable.
Objective
In general, the goal of a distributed system is to always proceed toward the correct decision, which results in two properties that determine the efficiency of the protocols used:
- Safety: the decision chosen is always correct.
- Liveness: the protocol always allows a decision to be reached.
As we shall see, in the next article there is a theorem that tells us that in an asynchronous system with crash-prone processes it is not possible to have both properties. As needed, there needs to be a tradeoff between the two.
Space-time diagram
Okay, let’s move on to something a little more serious: how do we graphically represent a distributed computation? You can use a diagram that some people call a space-time diagram, which has this form:

At a first glance what do we understand?
- There are 3 processes called $p_k$.
- In each event there are events called $e_k^i$, where $k$ is the process number and $i$ is the event number within it.
- All events are labeled in this way.
- Some event pairs have an arrow: they are message exchanges; other events do not interact with other processes.
- Time flows.
We can immediately fix these two rules:
- If $i < j$, then $e_k^i \rightarrow e_k^j$.
- If $e$ is a sending event of message $m$ and $e’$ is the receiving event of $m$, then $e \rightarrow e'$
System cuts
We have a distributed system doing things, and at some point in time we somehow want to know the state of it: we need some protocol to make a snapshot, but before we talk about it in detail we need to understand some preparatory concepts, namely:
- What is a global state.
- What is a local state.
- What is a cut.
- Consistency of cuts.
Each process has its own history, for example in the above image $p_1$ can be represented by ${e_1^1,e_1^2,e_1^3}$: this is its local state. Formally, the local state of process $k$ is defined as $\sigma_k^n = e_k^1, …,e_k^n$.
If we combine all the local states of the processes in the system, surprise, we get the global state, defined as $\sigma = (\sigma_1,…,\sigma_i) \space \forall p_{1,…,n}$.
A cut is nothing more than a particular global state at a particular instant. When we take a snapshot, we get a cut.

A cut is the graphical representation of the global state: everything on the left is in the state; everything on the right has not happened yet.
In the image there is a very fortunate situation, that is, in which the obtained cut is accurate. This can only be achieved if the system is synchronous, that is, when all processes have a “synchronized clock” on which they can rely. But we want to deal with asynchronous systems, where a typical cut might look like this:
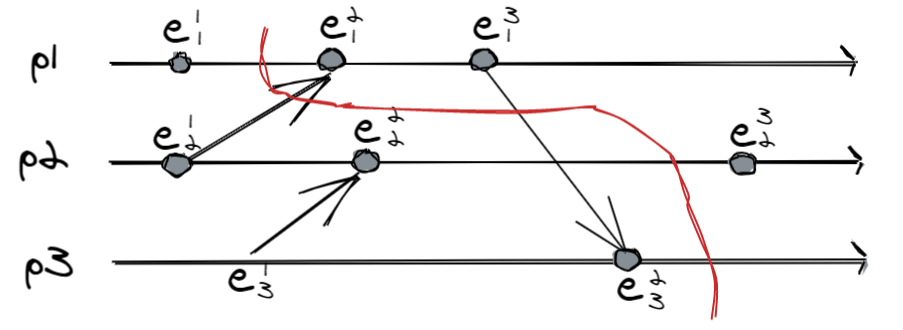
This cut is problematic, because it is inconsistent: we have captured a receive event $e_3^2$ but not the related send $e_1^3$. An inconsistent cut is a bit like a picture of an event that happened, but without the cause.

An inconsistent cut (or global inconsistent state, inconsistent cut) is a bit like seeing this picture, but with the ball stationary on the puck: it can’t happen. The whole system is in the state where the ball has been kicked and the goalkeeper has taken a dive, but the captured photo still shows the ball stationary (laughed).
Formally, a $C$ cut is consistent if $e \rightarrow e’ \wedge e’ \in C \Rightarrow e \in C$. Among friends, if in the cut you have the receiving event, you must also have the sending event.
Consistent snapshots thanks to Chandy and Lamport
Okay, how can we make snapshots always consistent? There is the nice Chandy-Lamport protocol that guarantees us that, assuming:
- Channels are FIFO: $send_i(m) \rightarrow send_i(m’) \Rightarrow delivery_j(m) \rightarrow delivery_j(m’)$
- Channels satisfy causal delivery: $send_i(m) \rightarrow send_j(m’) \Rightarrow deliver_k(m) \rightarrow deliver_k(m’)$.
Where $send$ and $delivery$ are the send and receive events, respectively.
The causal delivery is nothing but a FIFO between pairs of processes, and thus makes sure that messages are evaluated in the right order even at the receiving end.
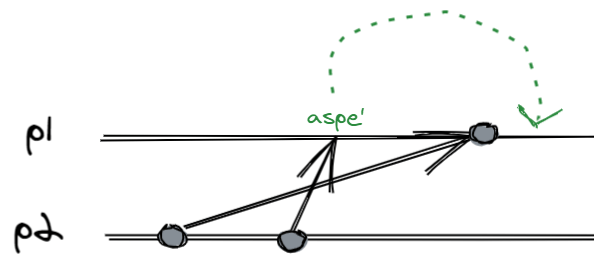
Chandy-Lamport snapshot protocol
This protocol always builds consistent snapshots, and to simplify it works like this:
- There is a monitor process that we call $p_0$.
- All the processes know each other.
- The monitor starts the protocol by broadcasting a marker message, which means “take the snapshot.”
- Each process, upon receiving the marker:
- If it is the first to receive, takes the snapshot and forwards the marker to all other processes.
- Otherwise, it stops listening to the one that sent it, and adds to the snapshot any events whose reception occurred between the previous and current marker.

The reason why this protocol always constructs consistent global states is precisely in the two assumptions:
- FIFO channels.
- Causal delivery.
In fact, it is not possible to have such a snapshot:
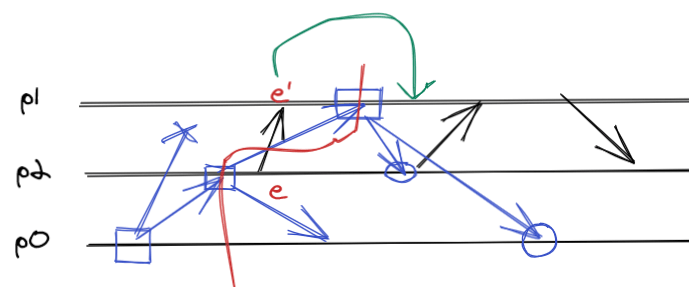
Precisely because $e’$ would be excluded from the picture, because it would be evaluated after the instant $p_1$ executes the snapshot.
Vector clock
Okay, all nice. We talked about some concepts in a somewhat abstract way: for example, we said that causal delivery is a rule whereby events are evaluated in the right order even at the receiving end; that’s beautiful, but how does it happen in practice? How does a process know the order of events of other processes?
Here, a cool way to do this is to use vector clocks, that is, an efficient system for labeling events in such a way that the order is unique and understandable among different processes. We can see vector clocks as a timestamp mechanism.

It is easier to infer the rules by looking at the image instead of formally writing them down, but still each process:
- Maintains a vector in which each position corresponds to a process in the system.
- Initializes all positions to $0$.
- Increments its position with each local event.
- Attaches the vector to each send event.
- Compares the received vector with the current one, and takes the largest values.
In a sense, vector clocks tell us what each process knows about all the others.
Vector clocks also give us seven nice properties, the most interesting of which are:
Strong clock condition
Let $VC(e)$ be the value of the vector at the instant of event $e$:
$e \rightarrow is \Leftrightarrow VC(e) < VC(e’)$.
Simple strong clock condition
$e_i \rightarrow e_j \Leftrightarrow VC(e_i)[i] \le VC(e_j)[i]$
Weak gap detection
$VC(e_i)[k] < VC(e_j)[k] \wedge k \ne j \Rightarrow \exists e_k \space | \space e_k \not\rightarrow e_i \wedge e_k \rightarrow e_j$
Informally, by observing two vectors in $e_i$ and $e_j$ on the respective distinct processes $p_i$ and $p_j$, one can tell whether there was an event on another process $p_k$ that $p_j$ knows about but not $p_i$.
Conclusion
Perfect, these are the basic concepts for being able to reason about distributed systems. We realized that working on asynchronous systems is not trivial, and that an example of this difficulty is querying all processes to understand the global state of the system.
This led us to the concept of cutting and coherence.
We saw a protocol for getting always consistent snapshots, which was brought up by two little people called Chandy and Lamport.
Finally we saw a real mechanism for labeling events by vector clock, and some interesting properties.
Posts in this series
- Paxos: A Distributed Consensus Protocol
- Distributed Consensus, Atomic Commit and FLP Theorem
- Basics of Distributed Systems Theory